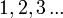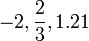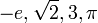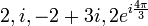Bahan Ajar dan Bank Soal Matematika

Jumat, 11 November 2011

Georg Ferdinand Ludwig Philipp Cantor

Born: 3 March 1845 in St Petersburg, Russia Died: 6 Jan 1918 in Halle, Germany

Click the picture above
to see four larger pictures

Previous	(Chronologically)	Next	Main Index
Previous	(Alphabetically)	Next	Biographies index

Version for printing

Georg Cantor's father, Georg Waldemar Cantor, was a successful merchant, working as a wholesaling agent in St Petersburg, then later as a broker in the St Petersburg Stock Exchange. Georg Waldemar Cantor was born in Denmark and he was a man with a deep love of culture and the arts. Georg's mother, Maria Anna Böhm, was Russian and very musical. Certainly Georg inherited considerable musical and artistic talents from his parents being an outstanding violinist. Georg was brought up a Protestant, this being the religion of his father, while Georg's mother was a Roman Catholic.

After early education at home from a private tutor, Cantor attended primary school in St Petersburg, then in 1856 when he was eleven years old the family moved to Germany. However, Cantor [21]:-

... remembered his early years in Russia with great nostalgia and never felt at ease in Germany, although he lived there for the rest of his life and seemingly never wrote in the Russian language, which he must have known.

Cantor's father had poor health and the move to Germany was to find a warmer climate than the harsh winters of St Petersburg. At first they lived in Wiesbaden, where Cantor attended the Gymnasium, then they moved to Frankfurt. Cantor studied at the Realschule in Darmstadt where he lived as a boarder. He graduated in 1860 with an outstanding report, which mentioned in particular his exceptional skills in mathematics, in particular trigonometry. After attending the Höhere Gewerbeschule in Darmstadt from 1860 he entered the Polytechnic of Zurich in 1862. The reason Cantor's father chose to send him to the Höheren Gewerbeschule was that he wanted Cantor to become:-

... a shining star in the engineering firmament.

However, in 1862 Cantor had sought his father's permission to study mathematics at university and he was overjoyed when eventually his father consented. His studies at Zurich, however, were cut short by the death of his father in June 1863. Cantor moved to the University of Berlin where he became friends with Hermann Schwarz who was a fellow student. Cantor attended lectures by Weierstrass, Kummer and Kronecker. He spent the summer term of 1866 at the University of Göttingen, returning to Berlin to complete his dissertation on number theory De aequationibus secundi gradus indeterminatis in 1867.

While at Berlin Cantor became much involved with the Mathematical Society being president of the Society during 1864-65. He was also part of a small group of young mathematicians who met weekly in a wine house. After receiving his doctorate in 1867, Cantor taught at a girl's school in Berlin. Then, in 1868, he joined the Schellbach Seminar for mathematics teachers. During this time he worked on his habilitation and, immediately after being appointed to Halle in 1869, he presented his thesis, again on number theory, and received his habilitation.

At Halle the direction of Cantor's research turned away from number theory and towards analysis. This was due to Heine, one of his senior colleagues at Halle, who challenged Cantor to prove the open problem on the uniqueness of representation of a function as a trigonometric series. This was a difficult problem which had been unsuccessfully attacked by many mathematicians, including Heine himself as well as Dirichlet, Lipschitz and Riemann. Cantor solved the problem proving uniqueness of the representation by April 1870. He published further papers between 1870 and 1872 dealing with trigonometric series and these all show the influence of Weierstrass's teaching.

Cantor was promoted to Extraordinary Professor at Halle in 1872 and in that year he began a friendship with Dedekind who he had met while on holiday in Switzerland. Cantor published a paper on trigonometric series in 1872 in which he defined irrational numbers in terms of convergent sequences of rational numbers. Dedekind published his definition of the real numbers by "Dedekind cuts" also in 1872 and in this paper Dedekind refers to Cantor's 1872 paper which Cantor had sent him.

In 1873 Cantor proved the rational numbers countable, i.e. they may be placed in one-one correspondence with the natural numbers. He also showed that the algebraic numbers, i.e. the numbers which are roots of polynomial equations with integer coefficients, were countable. However his attempts to decide whether the real numbers were countable proved harder. He had proved that the real numbers were not countable by December 1873 and published this in a paper in 1874. It is in this paper that the idea of a one-one correspondence appears for the first time, but it is only implicit in this work.

A transcendental number is an irrational number that is not a root of any polynomial equation with integer coefficients. Liouville established in 1851 that transcendental numbers exist. Twenty years later, in this 1874 work, Cantor showed that in a certain sense 'almost all' numbers are transcendental by proving that the real numbers were not countable while he had proved that the algebraic numbers were countable.

Cantor pressed forward, exchanging letters throughout with Dedekind. The next question he asked himself, in January 1874, was whether the unit square could be mapped into a line of unit length with a 1-1 correspondence of points on each. In a letter to Dedekind dated 5 January 1874 he wrote [1]:-

Can a surface (say a square that includes the boundary) be uniquely referred to a line (say a straight line segment that includes the end points) so that for every point on the surface there is a corresponding point of the line and, conversely, for every point of the line there is a corresponding point of the surface? I think that answering this question would be no easy job, despite the fact that the answer seems so clearly to be "no" that proof appears almost unnecessary.

The year 1874 was an important one in Cantor's personal life. He became engaged to Vally Guttmann, a friend of his sister, in the spring of that year. They married on 9 August 1874 and spent their honeymoon in Interlaken in Switzerland where Cantor spent much time in mathematical discussions with Dedekind.

Cantor continued to correspond with Dedekind, sharing his ideas and seeking Dedekind's opinions, and he wrote to Dedekind in 1877 proving that there was a 1-1 correspondence of points on the interval [0, 1] and points in p-dimensional space. Cantor was surprised at his own discovery and wrote:-

I see it, but I don't believe it!

Of course this had implications for geometry and the notion of dimension of a space. A major paper on dimension which Cantor submitted to Crelle's Journal in 1877 was treated with suspicion by Kronecker, and only published after Dedekind intervened on Cantor's behalf. Cantor greatly resented Kronecker's opposition to his work and never submitted any further papers to Crelle's Journal.

The paper on dimension which appeared in Crelle's Journal in 1878 makes the concepts of 1-1 correspondence precise. The paper discusses denumerable sets, i.e. those which are in 1-1 correspondence with the natural numbers. It studies sets of equal power, i.e. those sets which are in 1-1 correspondence with each other. Cantor also discussed the concept of dimension and stressed the fact that his correspondence between the interval [0, 1] and the unit square was not a continuous map.

Between 1879 and 1884 Cantor published a series of six papers in Mathematische Annalen designed to provide a basic introduction to set theory. Klein may have had a major influence in having Mathematische Annalen published them. However there were a number of problems which occurred during these years which proved difficult for Cantor. Although he had been promoted to a full professor in 1879 on Heine's recommendation, Cantor had been hoping for a chair at a more prestigious university. His long standing correspondence with Schwarz ended in 1880 as opposition to Cantor's ideas continued to grow and Schwarz no longer supported the direction that Cantor's work was going. Then in October 1881 Heine died and a replacement was needed to fill the chair at Halle.

Cantor drew up a list of three mathematicians to fill Heine's chair and the list was approved. It placed Dedekind in first place, followed by Heinrich Weber and finally Mertens. It was certainly a severe blow to Cantor when Dedekind declined the offer in the early 1882, and the blow was only made worse by Heinrich Weber and then Mertens declining too. After a new list had been drawn up, Wangerin was appointed but he never formed a close relationship with Cantor. The rich mathematical correspondence between Cantor and Dedekind ended later in 1882.

Almost the same time as the Cantor-Dedekind correspondence ended, Cantor began another important correspondence with Mittag-Leffler. Soon Cantor was publishing in Mittag-Leffler's journal Acta Mathematica but his important series of six papers in Mathematische Annalen also continued to appear. The fifth paper in this series Grundlagen einer allgemeinen Mannigfaltigkeitslehre was also published as a separate monograph and was especially important for a number of reasons. Firstly Cantor realised that his theory of sets was not finding the acceptance that he had hoped and the Grundlagen was designed to reply to the criticisms. Secondly [3]:-

The major achievement of the Grundlagen was its presentation of the transfinite numbers as an autonomous and systematic extension of the natural numbers.

Cantor himself states quite clearly in the paper that he realises the strength of the opposition to his ideas:-

... I realise that in this undertaking I place myself in a certain opposition to views widely held concerning the mathematical infinite and to opinions frequently defended on the nature of numbers.

At the end of May 1884 Cantor had the first recorded attack of depression. He recovered after a few weeks but now seemed less confident. He wrote to Mittag-Leffler at the end of June [3]:-

... I don't know when I shall return to the continuation of my scientific work. At the moment I can do absolutely nothing with it, and limit myself to the most necessary duty of my lectures; how much happier I would be to be scientifically active, if only I had the necessary mental freshness.

At one time it was thought that his depression was caused by mathematical worries and as a result of difficulties of his relationship with Kronecker in particular. Recently, however, a better understanding of mental illness has meant that we can now be certain that Cantor's mathematical worries and his difficult relationships were greatly magnified by his depression but were not its cause (see for example [3] and [21]). After this mental illness of 1884 [3]:-

... he took a holiday in his favourite Harz mountains and for some reason decided to try to reconcile himself with Kronecker. Kronecker accepted the gesture, but it must have been difficult for both of them to forget their enmities and the philosophical disagreements between them remained unaffected.

Mathematical worries began to trouble Cantor at this time, in particular he began to worry that he could not prove the continuum hypothesis, namely that the order of infinity of the real numbers was the next after that of the natural numbers. In fact he thought he had proved it false, then the next day found his mistake. Again he thought he had proved it true only again to quickly find his error.

All was not going well in other ways too, for in 1885 Mittag-Leffler persuaded Cantor to withdraw one of his papers from Acta Mathematica when it had reached the proof stage because he thought it "... about one hundred years too soon". Cantor joked about it but was clearly hurt:-

Had Mittag-Leffler had his way, I should have to wait until the year 1984, which to me seemed too great a demand! ... But of course I never want to know anything again about Acta Mathematica.

Mittag-Leffler meant this as a kindness but it does show a lack of appreciation of the importance of Cantor's work. The correspondence between Mittag-Leffler and Cantor all but stopped shortly after this event and the flood of new ideas which had led to Cantor's rapid development of set theory over about 12 years seems to have almost stopped.

In 1886 Cantor bought a fine new house on Händelstrasse, a street named after the German composer Handel. Before the end of the year a son was born, completing his family of six children. He turned from the mathematical development of set theory towards two new directions, firstly discussing the philosophical aspects of his theory with many philosophers (he published these letters in 1888) and secondly taking over after Clebsch's death his idea of founding the Deutsche Mathematiker-Vereinigung which he achieved in 1890. Cantor chaired the first meeting of the Association in Halle in September 1891, and despite the bitter antagonism between himself and Kronecker, Cantor invited Kronecker to address the first meeting.

Kronecker never addressed the meeting, however, since his wife was seriously injured in a climbing accident in the late summer and died shortly afterwards. Cantor was elected president of the Deutsche Mathematiker-Vereinigung at the first meeting and held this post until 1893. He helped to organise the meeting of the Association held in Munich in September 1893, but he took ill again before the meeting and could not attend.

Cantor published a rather strange paper in 1894 which listed the way that all even numbers up to 1000 could be written as the sum of two primes. Since a verification of Goldbach's conjecture up to 10000 had been done 40 years before, it is likely that this strange paper says more about Cantor's state of mind than it does about Goldbach's conjecture.

His last major papers on set theory appeared in 1895 and 1897, again in Mathematische Annalen under Klein's editorship, and are fine surveys of transfinite arithmetic. The rather long gap between the two papers is due to the fact that although Cantor finished writing the second part six months after the first part was published, he hoped to include a proof of the continuum hypothesis in the second part. However, it was not to be, but the second paper describes his theory of well-ordered sets and ordinal numbers.

In 1897 Cantor attended the first International Congress of Mathematicians in Zurich. In their lectures at the Congress [4]:-

... Hurwitz openly expressed his great admiration of Cantor and proclaimed him as one by whom the theory of functions has been enriched. Jacques Hadamard expressed his opinion that the notions of the theory of sets were known and indispensable instruments.

At the Congress Cantor met Dedekind and they renewed their friendship. By the time of the Congress, however, Cantor had discovered the first of the paradoxes in the theory of sets. He discovered the paradoxes while working on his survey papers of 1895 and 1897 and he wrote to Hilbert in 1896 explaining the paradox to him. Burali-Forti discovered the paradox independently and published it in 1897. Cantor began a correspondence with Dedekind to try to understand how to solve the problems but recurring bouts of his mental illness forced him to stop writing to Dedekind in 1899.

Whenever Cantor suffered from periods of depression he tended to turn away from mathematics and turn towards philosophy and his big literary interest which was a belief that Francis Bacon wrote Shakespeare's plays. For example in his illness of 1884 he had requested that he be allowed to lecture on philosophy instead of mathematics and he had begun his intense study of Elizabethan literature in attempting to prove his Bacon-Shakespeare theory. He began to publish pamphlets on the literary question in 1896 and 1897. Extra stress was put on Cantor with the death of his mother in October 1896 and the death of his younger brother in January 1899.

In October 1899 Cantor applied for, and was granted, leave from teaching for the winter semester of 1899-1900. Then on 16 December 1899 Cantor's youngest son died. From this time on until the end of his life he fought against the mental illness of depression. He did continue to teach but also had to take leave from his teaching for a number of winter semesters, those of 1902-03, 1904-05 and 1907-08. Cantor also spent some time in sanatoria, at the times of the worst attacks of his mental illness, from 1899 onwards. He did continue to work and publish on his Bacon-Shakespeare theory and certainly did not give up mathematics completely. He lectured on the paradoxes of set theory to a meeting of the Deutsche Mathematiker-Vereinigung in September 1903 and he attended the International Congress of Mathematicians at Heidelberg in August 1904.

In 1905 Cantor wrote a religious work after returning home from a spell in hospital. He also corresponded with Jourdain on the history of set theory and his religious tract. After taking leave for much of 1909 on the grounds of his ill health he carried out his university duties for 1910 and 1911. It was in that year that he was delighted to receive an invitation from the University of St Andrews in Scotland to attend the 500^th anniversary of the founding of the University as a distinguished foreign scholar. The celebrations were 12-15 September 1911 but [21]:-

During the visit he apparently began to behave eccentrically, talking at great length on the Bacon-Shakespeare question; then he travelled down to London for a few days.

Cantor had hoped to meet with Russell who had just published the Principia Mathematica. However ill health and the news that his son had taken ill made Cantor return to Germany without seeing Russell. The following year Cantor was awarded the honorary degree of Doctor of Laws by the University of St Andrews but he was too ill to receive the degree in person.

Cantor retired in 1913 and spent his final years ill with little food because of the war conditions in Germany. A major event planned in Halle to mark Cantor's 70 th birthday in 1915 had to be cancelled because of the war, but a smaller event was held in his home. In June 1917 he entered a sanatorium for the last time and continually wrote to his wife asking to be allowed to go home. He died of a heart attack.

Hilbert described Cantor's work as:-

...the finest product of mathematical genius and one of the supreme achievements of purely intellectual human activity.

Article by: J J O'Connor and E F Robertson
Click on this link to see a list of the Glossary entries for this page

List of References (36 books/articles)	Some Quotations (9)
Mathematicians born in the same country

Additional Material in MacTutor

Philip Jourdain and Georg Cantor
Extract from Cantor's Über einen die trigonometrischen Reihen betreffenden Lehrsatz which is one of his first publications on the theory of functions.
Extract from Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen containing the first (1874) proof of the uncountability of the Reals.
Extract from Über unendliche lineare Punktmannigfultigkeiten .


Honours awarded to Georg Cantor (Click below for those honoured in this way)
LMS Honorary Member	1901
Royal Society Sylvester Medal	1904
Fellow of the Royal Society of Edinburgh	1905
Lunar features	Crater Cantor
Popular biographies list	Number 32

Cross-references in MacTutor

Other Web sites
Encyclopaedia Britannica Astroseti (A Spanish translation of this biography)	Mathematical Genealogy Project

Previous	(Chronologically)	Next	Main Index
Previous	(Alphabetically)	Next	Biographies index
History Topics	Societies, honours, etc.		Famous curves
Time lines	Birthplace maps	Chronology	Search Form
Glossary index	Quotations index		Poster index
Mathematicians of the day		Anniversaries for the year

JOC/EFR © October 1998 Copyright information	School of Mathematics and Statistics University of St Andrews, Scotland
The URL of this page is: http://www-history.mcs.st-andrews.ac.uk/Biographies/Cantor.html

Kamis, 10 November 2011

Gottfried Wilhelm von Leibniz

Born: 1 July 1646 in Leipzig, Saxony (now Germany)

Died: 14 Nov 1716 in Hannover, Hanover (now Germany)

Click the picture above

to see eight larger pictures

Show birthplace location

Previous	(Chronologically)	Next	Main Index
Previous	(Alphabetically)	Next	Biographies index

Version for printing

Gottfried Leibniz was the son of Friedrich Leibniz, a professor of moral philosophy at Leipzig. Friedrich Leibniz [3]:-

...was evidently a competent though not original scholar, who devoted his time to his offices and to his family as a pious, Christian father.

Leibniz's mother was Catharina Schmuck, the daughter of a lawyer and Friedrich Leibniz's third wife. However, Friedrich Leibniz died when Leibniz was only six years old and he was brought up by his mother. Certainly Leibniz learnt his moral and religious values from her which would play an important role in his life and philosophy.

At the age of seven, Leibniz entered the Nicolai School in Leipzig. Although he was taught Latin at school, Leibniz had taught himself far more advanced Latin and some Greek by the age of 12. He seems to have been motivated by wanting to read his father's books. As he progressed through school he was taught Aristotle's logic and theory of categorising knowledge. Leibniz was clearly not satisfied with Aristotle's system and began to develop his own ideas on how to improve on it. In later life Leibniz recalled that at this time he was trying to find orderings on logical truths which, although he did not know it at the time, were the ideas behind rigorous mathematical proofs. As well as his school work, Leibniz studied his father's books. In particular he read metaphysics books and theology books from both Catholic and Protestant writers.

In 1661, at the age of fourteen, Leibniz entered the University of Leipzig. It may sound today as if this were a truly exceptionally early age for anyone to enter university, but it is fair to say that by the standards of the time he was quite young but there would be others of a similar age. He studied philosophy, which was well taught at the University of Leipzig, and mathematics which was very poorly taught. Among the other topics which were included in this two year general degree course were rhetoric, Latin, Greek and Hebrew. He graduated with a bachelors degree in 1663 with a thesis De Principio Individui (On the Principle of the Individual) which:-

... emphasised the existential value of the individual, who is not to be explained either by matter alone or by form alone but rather by his whole being.

In this there is the beginning of his notion of "monad". Leibniz then went to Jena to spend the summer term of 1663.

At Jena the professor of mathematics was Erhard Weigel but Weigel was also a philosopher and through him Leibniz began to understand the importance of the method of mathematical proof for subjects such as logic and philosophy. Weigel believed that number was the fundamental concept of the universe and his ideas were to have considerable influence of Leibniz. By October 1663 Leibniz was back in Leipzig starting his studies towards a doctorate in law. He was awarded his Master's Degree in philosophy for a dissertation which combined aspects of philosophy and law studying relations in these subjects with mathematical ideas that he had learnt from Weigel. A few days after Leibniz presented his dissertation, his mother died.

After being awarded a bachelor's degree in law, Leibniz worked on his habilitation in philosophy. His work was to be published in 1666 as Dissertatio de arte combinatoria (Dissertation on the combinatorial art). In this work Leibniz aimed to reduce all reasoning and discovery to a combination of basic elements such as numbers, letters, sounds and colours.

Despite his growing reputation and acknowledged scholarship, Leibniz was refused the doctorate in law at Leipzig. It is a little unclear why this happened. It is likely that, as one of the younger candidates and there only being twelve law tutorships available, he would be expected to wait another year. However, there is also a story that the Dean's wife persuaded the Dean to argue against Leibniz, for some unexplained reason. Leibniz was not prepared to accept any delay and he went immediately to the University of Altdorf where he received a doctorate in law in February 1667 for his dissertation De Casibus Perplexis (On Perplexing Cases).

Leibniz declined the promise of a chair at Altdorf because he had very different things in view. He served as secretary to the Nuremberg alchemical society for a while (see [187]) then he met Baron Johann Christian von Boineburg. By November 1667 Leibniz was living in Frankfurt, employed by Boineburg. During the next few years Leibniz undertook a variety of different projects, scientific, literary and political. He also continued his law career taking up residence at the courts of Mainz before 1670. One of his tasks there, undertaken for the Elector of Mainz, was to improve the Roman civil law code for Mainz but [3]:-

Leibniz was also occupied by turns as Boineburg's secretary, assistant, librarian, lawyer and advisor, while at the same time a personal friend of the Baron and his family.

Boineburg was a Catholic while Leibniz was a Lutheran but Leibniz had as one of his lifelong aims the reunification of the Christian Churches and [30]:-

... with Boineburg's encouragement, he drafted a number of monographs on religious topics, mostly to do with points at issue between the churches...

Another of Leibniz's lifelong aims was to collate all human knowledge. Certainly he saw his work on Roman civil law as part of this scheme and as another part of this scheme, Leibniz tried to bring the work of the learned societies together to coordinate research. Leibniz began to study motion, and although he had in mind the problem of explaining the results of Wren and Huygens on elastic collisions, he began with abstract ideas of motion. In 1671 he published Hypothesis Physica Nova (New Physical Hypothesis). In this work he claimed, as had Kepler, that movement depends on the action of a spirit. He communicated with Oldenburg, the secretary of the Royal Society of London, and dedicated some of his scientific works to the Royal Society and the Paris Academy. Leibniz was also in contact with Carcavi, the Royal Librarian in Paris. As Ross explains in [30]:-

Although Leibniz's interests were clearly developing in a scientific direction, he still hankered after a literary career. All his life he prided himself on his poetry (mostly Latin), and boasted that he could recite the bulk of Virgil's "Aeneid" by heart. During this time with Boineburg he would have passed for a typical late Renaissance humanist.

Leibniz wished to visit Paris to make more scientific contacts. He had begun construction of a calculating machine which he hoped would be of interest. He formed a political plan to try to persuade the French to attack Egypt and this proved the means of his visiting Paris. In 1672 Leibniz went to Paris on behalf of Boineburg to try to use his plan to divert Louis XIV from attacking German areas. His first object in Paris was to make contact with the French government but, while waiting for such an opportunity, Leibniz made contact with mathematicians and philosophers there, in particular Arnauld and Malebranche, discussing with Arnauld a variety of topics but particularly church reunification.

In Paris Leibniz studied mathematics and physics under Christiaan Huygens beginning in the autumn of 1672. On Huygens' advice, Leibniz read Saint-Vincent's work on summing series and made some discoveries of his own in this area. Also in the autumn of 1672, Boineburg's son was sent to Paris to study under Leibniz which meant that his financial support was secure. Accompanying Boineburg's son was Boineburg's nephew on a diplomatic mission to try to persuade Louis XIV to set up a peace congress. Boineburg died on 15 December but Leibniz continued to be supported by the Boineburg family.

In January 1673 Leibniz and Boineburg's nephew went to England to try the same peace mission, the French one having failed. Leibniz visited the Royal Society, and demonstrated his incomplete calculating machine. He also talked with Hooke, Boyle and Pell. While explaining his results on series to Pell, he was told that these were to be found in a book by Mouton. The next day he consulted Mouton's book and found that Pell was correct. At the meeting of the Royal Society on 15 February, which Leibniz did not attend, Hooke made some unfavourable comments on Leibniz's calculating machine. Leibniz returned to Paris on hearing that the Elector of Mainz had died. Leibniz realised that his knowledge of mathematics was less than he would have liked so he redoubled his efforts on the subject.

The Royal Society of London elected Leibniz a fellow on 19 April 1673. Leibniz met Ozanam and solved one of his problems. He also met again with Huygens who gave him a reading list including works by Pascal, Fabri, Gregory, Saint-Vincent, Descartes and Sluze. He began to study the geometry of infinitesimals and wrote to Oldenburg at the Royal Society in 1674. Oldenburg replied that Newton and Gregory had found general methods. Leibniz was, however, not in the best of favours with the Royal Society since he had not kept his promise of finishing his mechanical calculating machine. Nor was Oldenburg to know that Leibniz had changed from the rather ordinary mathematician who visited London, into a creative mathematical genius. In August 1675 Tschirnhaus arrived in Paris and he formed a close friendship with Leibniz which proved very mathematically profitable to both.

It was during this period in Paris that Leibniz developed the basic features of his version of the calculus. In 1673 he was still struggling to develop a good notation for his calculus and his first calculations were clumsy. On 21 November 1675 he wrote a manuscript using the ∫ f (x) dx notation for the first time. In the same manuscript the product rule for differentiation is given. By autumn 1676 Leibniz discovered the familiar d(xⁿ) = nx^n-1dx for both integral and fractional n.

Newton wrote a letter to Leibniz, through Oldenburg, which took some time to reach him. The letter listed many of Newton's results but it did not describe his methods. Leibniz replied immediately but Newton, not realising that his letter had taken a long time to reach Leibniz, thought he had had six weeks to work on his reply. Certainly one of the consequences of Newton's letter was that Leibniz realised he must quickly publish a fuller account of his own methods.

Newton wrote a second letter to Leibniz on 24 October 1676 which did not reach Leibniz until June 1677 by which time Leibniz was in Hanover. This second letter, although polite in tone, was clearly written by Newton believing that Leibniz had stolen his methods. In his reply Leibniz gave some details of the principles of his differential calculus including the rule for differentiating a function of a function.

Newton was to claim, with justification, that

... not a single previously unsolved problem was solved ...

by Leibniz's approach but the formalism was to prove vital in the latter development of the calculus. Leibniz never thought of the derivative as a limit. This does not appear until the work of d'Alembert.

Leibniz would have liked to have remained in Paris in the Academy of Sciences, but it was considered that there were already enough foreigners there and so no invitation came. Reluctantly Leibniz accepted a position from the Duke of Hanover, Johann Friedrich, of librarian and of Court Councillor at Hanover. He left Paris in October 1676 making the journey to Hanover via London and Holland. The rest of Leibniz's life, from December 1676 until his death, was spent at Hanover except for the many travels that he made.

His duties at Hanover [30]:-

... as librarian were onerous, but fairly mundane: general administration, purchase of new books and second-hand libraries, and conventional cataloguing.

He undertook a whole collection of other projects however. For example one major project begun in 1678-79 involved draining water from the mines in the Harz mountains. His idea was to use wind power and water power to operate pumps. He designed many different types of windmills, pumps, gears but [3]:-

... every one of these projects ended in failure. Leibniz himself believed that this was because of deliberate obstruction by administrators and technicians, and the workers' fear that technological progress would cost them their jobs.

In 1680 Duke Johann Friedrich died and his brother Ernst August became the new Duke. The Harz project had always been difficult and it failed by 1684. However Leibniz had achieved important scientific results becoming one of the first people to study geology through the observations he compiled for the Harz project. During this work he formed the hypothesis that the Earth was at first molten.

Another of Leibniz's great achievements in mathematics was his development of the binary system of arithmetic. He perfected his system by 1679 but he did not publish anything until 1701 when he sent the paper Essay d'une nouvelle science des nombres to the Paris Academy to mark his election to the Academy. Another major mathematical work by Leibniz was his work on determinants which arose from his developing methods to solve systems of linear equations. Although he never published this work in his lifetime, he developed many different approaches to the topic with many different notations being tried out to find the one which was most useful. An unpublished paper dated 22 January 1684 contains very satisfactory notation and results.

Leibniz continued to perfect his metaphysical system in the 1680s attempting to reduce reasoning to an algebra of thought. Leibniz published Meditationes de Cognitione, Veritate et Ideis (Reflections on Knowledge, Truth, and Ideas) which clarified his theory of knowledge. In February 1686, Leibniz wrote his Discours de métaphysique (Discourse on Metaphysics).

Another major project which Leibniz undertook, this time for Duke Ernst August, was writing the history of the Guelf family, of which the House of Brunswick was a part. He made a lengthy trip to search archives for material on which to base this history, visiting Bavaria, Austria and Italy between November 1687 and June 1690. As always Leibniz took the opportunity to meet with scholars of many different subjects on these journeys. In Florence, for example, he discussed mathematics with Viviani who had been Galileo's last pupil. Although Leibniz published nine large volumes of archival material on the history of the Guelf family, he never wrote the work that was commissioned.

In 1684 Leibniz published details of his differential calculus in Nova Methodus pro Maximis et Minimis, itemque Tangentibus... in Acta Eruditorum, a journal established in Leipzig two years earlier. The paper contained the familiar d notation, the rules for computing the derivatives of powers, products and quotients. However it contained no proofs and Jacob Bernoulli called it an enigma rather than an explanation.

In 1686 Leibniz published, in Acta Eruditorum, a paper dealing with the integral calculus with the first appearance in print of the ∫ notation.

Newton's Principia appeared the following year. Newton's 'method of fluxions' was written in 1671 but Newton failed to get it published and it did not appear in print until John Colson produced an English translation in 1736. This time delay in the publication of Newton's work resulted in a dispute with Leibniz.

Another important piece of mathematical work undertaken by Leibniz was his work on dynamics. He criticised Descartes' ideas of mechanics and examined what are effectively kinetic energy, potential energy and momentum. This work was begun in 1676 but he returned to it at various times, in particular while he was in Rome in 1689. It is clear that while he was in Rome, in addition to working in the Vatican library, Leibniz worked with members of the Accademia. He was elected a member of the Accademia at this time. Also while in Rome he read Newton's Principia. His two part treatise Dynamica studied abstract dynamics and concrete dynamics and is written in a somewhat similar style to Newton's Principia. Ross writes in [30]:-

... although Leibniz was ahead of his time in aiming at a genuine dynamics, it was this very ambition that prevented him from matching the achievement of his rival Newton. ... It was only by simplifying the issues... that Newton succeeded in reducing them to manageable proportions.

Leibniz put much energy into promoting scientific societies. He was involved in moves to set up academies in Berlin, Dresden, Vienna, and St Petersburg. He began a campaign for an academy in Berlin in 1695, he visited Berlin in 1698 as part of his efforts and on another visit in 1700 he finally persuaded Friedrich to found the Brandenburg Society of Sciences on 11 July. Leibniz was appointed its first president, this being an appointment for life. However, the Academy was not particularly successful and only one volume of the proceedings were ever published. It did lead to the creation of the Berlin Academy some years later.

Other attempts by Leibniz to found academies were less successful. He was appointed as Director of a proposed Vienna Academy in 1712 but Leibniz died before the Academy was created. Similarly he did much of the work to prompt the setting up of the St Petersburg Academy, but again it did not come into existence until after his death.

It is no exaggeration to say that Leibniz corresponded with most of the scholars in Europe. He had over 600 correspondents. Among the mathematicians with whom he corresponded was Grandi. The correspondence started in 1703, and later concerned the results obtained by putting x = 1 into 1/(1+x) = 1 - x + x² - x³ + .... Leibniz also corresponded with Varignon on this paradox. Leibniz discussed logarithms of negative numbers with Johann Bernoulli, see [155].

In 1710 Leibniz published Théodicée a philosophical work intended to tackle the problem of evil in a world created by a good God. Leibniz claims that the universe had to be imperfect, otherwise it would not be distinct from God. He then claims that the universe is the best possible without being perfect. Leibniz is aware that this argument looks unlikely - surely a universe in which nobody is killed by floods is better than the present one, but still not perfect. His argument here is that the elimination of natural disasters, for example, would involve such changes to the laws of science that the world would be worse. In 1714 Leibniz wrote Monadologia which synthesised the philosophy of his earlier work, the Théodicée.

Much of the mathematical activity of Leibniz's last years involved the priority dispute over the invention of the calculus. In 1711 he read the paper by Keill in the Transactions of the Royal Society of London which accused Leibniz of plagiarism. Leibniz demanded a retraction saying that he had never heard of the calculus of fluxions until he had read the works of Wallis. Keill replied to Leibniz saying that the two letters from Newton, sent through Oldenburg, had given:-

... pretty plain indications... whence Leibniz derived the principles of that calculus or at least could have derived them.

Leibniz wrote again to the Royal Society asking them to correct the wrong done to him by Keill's claims. In response to this letter the Royal Society set up a committee to pronounce on the priority dispute. It was totally biased, not asking Leibniz to give his version of the events. The report of the committee, finding in favour of Newton, was written by Newton himself and published as Commercium epistolicum near the beginning of 1713 but not seen by Leibniz until the autumn of 1714. He learnt of its contents in 1713 in a letter from Johann Bernoulli, reporting on the copy of the work brought from Paris by his nephew Nicolaus(I) Bernoulli. Leibniz published an anonymous pamphlet Charta volans setting out his side in which a mistake by Newton in his understanding of second and higher derivatives, spotted by Johann Bernoulli, is used as evidence of Leibniz's case.

The argument continued with Keill who published a reply to Charta volans. Leibniz refused to carry on the argument with Keill, saying that he could not reply to an idiot. However, when Newton wrote to him directly, Leibniz did reply and gave a detailed description of his discovery of the differential calculus. From 1715 up until his death Leibniz corresponded with Samuel Clarke, a supporter of Newton, on time, space, freewill, gravitational attraction across a void and other topics, see [4], [62], [108] and [201].

In [2] Leibniz is described as follows:-

Leibniz was a man of medium height with a stoop, broad-shouldered but bandy-legged, as capable of thinking for several days sitting in the same chair as of travelling the roads of Europe summer and winter. He was an indefatigable worker, a universal letter writer (he had more than 600 correspondents), a patriot and cosmopolitan, a great scientist, and one of the most powerful spirits of Western civilisation.

Ross, in [30], points out that Leibniz's legacy may have not been quite what he had hoped for:-

It is ironical that one so devoted to the cause of mutual understanding should have succeeded only in adding to intellectual chauvinism and dogmatism. There is a similar irony in the fact that he was one of the last great polymaths - not in the frivolous sense of having a wide general knowledge, but in the deeper sense of one who is a citizen of the whole world of intellectual inquiry. He deliberately ignored boundaries between disciplines, and lack of qualifications never deterred him from contributing fresh insights to established specialisms. Indeed, one of the reasons why he was so hostile to universities as institutions was because their faculty structure prevented the cross-fertilisation of ideas which he saw as essential to the advance of knowledge and of wisdom. The irony is that he was himself instrumental in bringing about an era of far greater intellectual and scientific specialism, as technical advances pushed more and more disciplines out of the reach of the intelligent layman and amateur.

Article by: J J O'Connor and E F Robertson
Click on this link to see a list of the Glossary entries for this page

List of References (228 books/articles)	Some Quotations (16)
Mathematicians born in the same country

Additional Material in MacTutor

Leibniz's calculating machine
Another picture of it.
Charles Bossut on Leibniz and Newton
A page from Leibnizens mathematische Schriften (published in 1850)


Honours awarded to Gottfried Leibniz (Click below for those honoured in this way)
Fellow of the Royal Society	1673
Lunar features	Crater Leibnitz
Paris street names	Rue Leibnitz and Square Leibnitz (18th Arrondissement)
Popular biographies list	Number 21

Cross-references in MacTutor

Other Web sites
Encyclopaedia Britannica Astroseti (A Spanish translation of this biography) NNDB The Galileo Project Bellevue College USA Rouse Ball Leibniz translations G Don Allen	Gregory Brown Don Rutherford Kevin Brown (Leibniz on computers) The Catholic Encyclopedia Internet Encyclopedia of Philosophy Stanford Encyclopedia of Philosophy Mathematical Genealogy Project

Previous	(Chronologically)	Next	Main Index
Previous	(Alphabetically)	Next	Biographies index
History Topics	Societies, honours, etc.		Famous curves
Time lines	Birthplace maps	Chronology	Search Form
Glossary index	Quotations index		Poster index
Mathematicians of the day		Anniversaries for the year

JOC/EFR © October 1998 Copyright information	School of Mathematics and Statistics University of St Andrews, Scotland
The URL of this page is: http://www-history.mcs.st-andrews.ac.uk/Biographies/Leibniz.html

Rabu, 09 November 2011

Biography Sir Isaac Newton

URL : http://www.biographyonline.net/scientists/isaac-newton.html

Early Life of Newton

Sir Isaac Newton was born on Christmas Day, in 1643, to a relatively poor farming family. His father died 3 months before he was born. His mother later remarried, but her second husband did not get on with Isaac; leading to friction between Isaac and his parents. The young Isaac attended school at King’s School, Grantham in Lincolnshire (where his signature is still inscribed in the walls.. Isaac was one of the top students, but before completing his studies his mother withdrew him from school, so Isaac could work as a farmer. It was only through the intervention of the headmaster that Isaac was able to return to finish his studies; he passed his final exams with very good results, and was able to go to Trinity College, Cambridge.

Newton at Cambridge

At Cambridge he was able to pursue his interests in mathematics, science and physics. At the time the prevailing education was based on Aristotle, but Isaac was more interested in modern mathematicians such as Descartes. Isaac Newton had a prodigious capacity to consider mathematical problems, and then focus on them until he had solved the mystery behind them. His one pointed nature led him to, at times, be detached from the world. For example, he had little time for women. An early teenage romance came to nothing, and he remained single throughout his life.

Sir Isaac Newton, has been referred to as one of the greatest genius’ of history. His mathematical and scientific achievements give credence to such a view. Amongst his many accomplishments in the field of science include:

Developing a theory of Calculus. Unfortunately, at the same time as Newton, calculus was being developed by Leibinz. When Leibinz published his results, there was a bitter feud between the two men, with Newton claiming plagiarism. This bitter feud lasted until Leibinz death in 1713, it also extended between British mathematicians and the continent.

Mathematical Achievements of Newton

generalized binomial theorem
Newton's identities,
Newton's method,
classified cubic plane curves (polynomials of degree three in two variables),
Substantial contributions to the theory of finite differences,
Use of fractional indices
Used geometry to derive solutions to Diophantine equations.
Used power series with confidence and to revert power series.
Discovered a new formula for pi.

Scientific Achievements of Newton

Optics – Newton made great advancements into the study of optics. In particular he developed the spectrum by splitting white light through a prism.
Telescope – Made significant improvements to the development of the telescope. However, when his ideas were criticised by Hooke, Newton withdrew from the public debate. He developed an antagonistic and hostile attitude to Hooke, throughout his life.
Mechanics and Gravitation. In his famous book Principa Mathematic. Newton explained the three laws of motion that laid the framework for modern physics. This involved explaining planetary movements.

Newton Hit on the Head with an Apple.

The most popular ante dote about Sir Isaac Newton is the story of how the theory of gravitation came to him, after being hit on the head with a falling apple. In reality, Newton and his friends may have exaggerated this story. Nevertheless, it is quite likely that seeing apples fall from trees may have influenced his theories of gravity.

Newton’s Religious Belief's

As well as being a scientist, Newton actually spent more time investigating religious issues. He read the Bible daily, believing it to be the word of God. Nevertheless, he was not satisfied with the Christian interpretations of the Bible. For example, he rejected the philosophy of the Holy Trinity, his beliefs were closer to the Christian beliefs in Arainism (basically there was a difference between Jesus Christ and God)

Newton - Bible Code

Newton was fascinated with the early Church and also the last chapter of the Bible Revelations. He spent many hours poring over the Bible, trying to find the secret Bible Code. He was rumoured to be a Rosicrucian. However, the religious belief’s that Newton held could have caused serious embarrassment at the time. Because of this he kept his views hidden, almost to the point of obsession. This desire for secrecy seemed to be part of his nature. It was only on his death that his papers were opened up. The bishop who first opened Newton’s box, actually found them too shocking for public release, therefore, they were kept closed for many more years.

Newton and Alchemy

Newton was also interested in alchemy. He experimented on many objects, using a lot of Mercury. Very high levels of mercury in his blood stream may have contributed to his early death and irregularities in later life.

Newton was made member of the Royal Society in 1703. He was also given the job of Master of Mint in 1717. He took this job seriously and unofficially was responsible for moving England from the silver standard to the gold standard.

Newton was an extraordinary polymath; the universe simply fascinated him. He sought to discover the hidden and outer mysteries of life. With his sharp intellect and powers of concentration, he was able to contribute to tremendous developments in many areas of science. He was a unique individual. John Maynard Keynes, a twentieth century genius, said of Newton:

“I do not think that any one who has pored over the contents of that box which he packed up when he finally left Cambridge in 1696 and which, though partly dispersed, have come down to us, can see him like that. Newton was not the first of the age of reason. He was the last of the magicians, the last of the Babylonians and Sumerians, the last great mind which looked out on the visible and intellectual world with the same eyes as those who began to build our intellectual inheritance rather less than 10,000 years ago. Isaac Newton, a posthumous child born with no father on Christmas Day, 1642, was the last wonderchild to whom the Magi could do sincere and appropriate homage.” [1]

Senin, 07 November 2011

Mathematics

URL : http://encyclopedia.thefreedictionary.com/Mathematics

Euclid, Greek mathematician, 3rd century BC, as imagined by Raphael in this detail from The School of Athens.^[1]

Mathematics is the study of quantity, structure, space, and change. Mathematicians seek out patterns,^[2]^[3] formulate new conjectures, and establish truth by rigorous deduction from appropriately chosen axioms and definitions.^[4]
There is debate over whether mathematical objects such as numbers and points exist naturally or are human creations. The mathematician Benjamin Peirce called mathematics "the science that draws necessary conclusions".^[5] Albert Einstein, on the other hand, stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."^[6]
Through the use of abstraction and logical reasoning, mathematics evolved from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. Mathematics continued to develop, for example in China in 300 BC, in India in AD 100, and in the Muslim world in AD 800, until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that continues to the present day.^[7]
Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind, although practical applications for what began as pure mathematics are often discovered.^[8]

Etymology

The word "mathematics" comes from the Greek μάθημα (máthēma), which means learning, study, science, and additionally came to have the narrower and more technical meaning "mathematical study", even in Classical times.^[9] Its adjective is μαθηματικός (mathēmatikós), related to learning, or studious, which likewise further came to mean mathematical. In particular, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), Latin: ars mathematica, meant the mathematical art.
The apparent plural form in English, like the French plural form les mathématiques (and the less commonly used singular derivative la mathématique), goes back to the Latin neuter plural mathematica (Cicero), based on the Greek plural τα μαθηματικά (ta mathēmatiká), used by Aristotle, and meaning roughly "all things mathematical"; although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics and metaphysics, which were inherited from the Greek.^[10] In English, the noun mathematics takes singular verb forms. It is often shortened to maths or, in English-speaking North America, math.

History

Main article: History of mathematics

Greek mathematician Pythagoras (c.570-c.495 BC), commonly credited with discovering the Pythagorean theorem.

The evolution of mathematics might be seen as an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction, which is shared by many animals,^[11] was probably that of numbers: the realization that a collection of two apples and a collection of two oranges (for example) have something in common, namely quantity of their members.
In addition to recognizing how to count physical objects, prehistoric peoples also recognized how to count abstract quantities, like time – days, seasons, years.^[12] Elementary arithmetic (addition, subtraction, multiplication and division) naturally followed.
Since numeracy pre-dated writing, further steps were needed for recording numbers such as tallies or the knotted strings called quipu used by the Inca to store numerical data.^{[citation needed]} Numeral systems have been many and diverse, with the first known written numerals created by Egyptians in Middle Kingdom texts such as the Rhind Mathematical Papyrus.^{[citation needed]}

Mayan numerals

The earliest uses of mathematics were in trading, land measurement, painting and weaving patterns and the recording of time. More complex mathematics did not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, for building and construction, and for astronomy.^[13] The systematic study of mathematics in its own right began with the Ancient Greeks between 600 and 300 BC.^[14]
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made today. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."^[15]

Inspiration, pure and applied mathematics, and aesthetics

Main article: Mathematical beauty

Sir Isaac Newton (1643-1727), an inventor of infinitesimal calculus.

Mathematics arises from many different kinds of problems. At first these were found in commerce, land measurement, architecture and later astronomy; nowadays, all sciences suggest problems studied by mathematicians, and many problems arise within mathematics itself. For example, the physicist Richard Feynman invented the path integral formulation of quantum mechanics using a combination of mathematical reasoning and physical insight, and today's string theory, a still-developing scientific theory which attempts to unify the four fundamental forces of nature, continues to inspire new mathematics.^[16] Some mathematics is only relevant in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts. A distinction is often made between pure mathematics and applied mathematics. However pure mathematics topics often turn out to have applications, e.g. number theory in cryptography. This remarkable fact that even the "purest" mathematics often turns out to have practical applications is what Eugene Wigner has called "the unreasonable effectiveness of mathematics".^[17] As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: there are now hundreds of specialized areas in mathematics and the latest Mathematics Subject Classification runs to 46 pages.^[18] Several areas of applied mathematics have merged with related traditions outside of mathematics and become disciplines in their own right, including statistics, operations research, and computer science.
For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof, such as Euclid's proof that there are infinitely many prime numbers, and in an elegant numerical method that speeds calculation, such as the fast Fourier transform. G. H. Hardy in A Mathematician's Apology expressed the belief that these aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. He identified criteria such as significance, unexpectedness, inevitability, and economy as factors that contribute to a mathematical aesthetic.^[19] Mathematicians often strive to find proofs of theorems that are particularly elegant, a quest Paul Erdős often referred to as finding proofs from "The Book" in which God had written down his favorite proofs.^[20]^[21] The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.

Notation, language, and rigor

Leonhard Euler, who created and popularized much of the mathematical notation used today

Main article: Mathematical notation

Most of the mathematical notation in use today was not invented until the 16th century.^[22] Before that, mathematics was written out in words, a painstaking process that limited mathematical discovery.^[23] Euler (1707–1783) was responsible for many of the notations in use today. Modern notation makes mathematics much easier for the professional, but beginners often find it daunting. It is extremely compressed: a few symbols contain a great deal of information. Like musical notation, modern mathematical notation has a strict syntax (which to a limited extent varies from author to author and from discipline to discipline) and encodes information that would be difficult to write in any other way.
Mathematical language can also be hard for beginners. Words such as or and only have more precise meanings than in everyday speech. Moreover, words such as open and field have been given specialized mathematical meanings. Mathematical jargon includes technical terms such as homeomorphism and integrable. But there is a reason for special notation and technical jargon: mathematics requires more precision than everyday speech. Mathematicians refer to this precision of language and logic as "rigor".

The infinity symbol ∞ in several typefaces.

Mathematical proof is fundamentally a matter of rigor. Mathematicians want their theorems to follow from axioms by means of systematic reasoning. This is to avoid mistaken "theorems", based on fallible intuitions, of which many instances have occurred in the history of the subject.^[24] The level of rigor expected in mathematics has varied over time: the Greeks expected detailed arguments, but at the time of Isaac Newton the methods employed were less rigorous. Problems inherent in the definitions used by Newton would lead to a resurgence of careful analysis and formal proof in the 19th century. Misunderstanding the rigor is a cause for some of the common misconceptions of mathematics. Today, mathematicians continue to argue among themselves about computer-assisted proofs. Since large computations are hard to verify, such proofs may not be sufficiently rigorous.^[25]
Axioms in traditional thought were "self-evident truths", but that conception is problematic. At a formal level, an axiom is just a string of symbols, which has an intrinsic meaning only in the context of all derivable formulas of an axiomatic system. It was the goal of Hilbert's program to put all of mathematics on a firm axiomatic basis, but according to Gödel's incompleteness theorem every (sufficiently powerful) axiomatic system has undecidable formulas; and so a final axiomatization of mathematics is impossible. Nonetheless mathematics is often imagined to be (as far as its formal content) nothing but set theory in some axiomatization, in the sense that every mathematical statement or proof could be cast into formulas within set theory.^[26]

Mathematics as science

Carl Friedrich Gauss, himself known as the "prince of mathematicians",^[27] referred to mathematics as "the Queen of the Sciences".

Carl Friedrich Gauss referred to mathematics as "the Queen of the Sciences".^[28] In the original Latin Regina Scientiarum, as well as in German Königin der Wissenschaften, the word corresponding to science means (field of) knowledge. Indeed, this is also the original meaning in English, and there is no doubt that mathematics is in this sense a science. The specialization restricting the meaning to natural science is of later date. If one considers science to be strictly about the physical world, then mathematics, or at least pure mathematics, is not a science. Albert Einstein stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."^[6]
Many philosophers believe that mathematics is not experimentally falsifiable, and thus not a science according to the definition of Karl Popper.^[29] However, in the 1930s Gödel's incompleteness theorems convinced many mathematicians that mathematics cannot be reduced to logic alone, and Karl Popper concluded that "most mathematical theories are, like those of physics and biology, hypothetico-deductive: pure mathematics therefore turns out to be much closer to the natural sciences whose hypotheses are conjectures, than it seemed even recently."^[30] Other thinkers, notably Imre Lakatos, have applied a version of falsificationism to mathematics itself.
An alternative view is that certain scientific fields (such as theoretical physics) are mathematics with axioms that are intended to correspond to reality. In fact, the theoretical physicist, J. M. Ziman, proposed that science is public knowledge and thus includes mathematics.^[31] In any case, mathematics shares much in common with many fields in the physical sciences, notably the exploration of the logical consequences of assumptions. Intuition and experimentation also play a role in the formulation of conjectures in both mathematics and the (other) sciences. Experimental mathematics continues to grow in importance within mathematics, and computation and simulation are playing an increasing role in both the sciences and mathematics, weakening the objection that mathematics does not use the scientific method.^{[citation needed]} In his 2002 book A New Kind of Science, Stephen Wolfram argues that computational mathematics deserves to be explored empirically as a scientific field in its own right.
The opinions of mathematicians on this matter are varied. Many mathematicians feel that to call their area a science is to downplay the importance of its aesthetic side, and its history in the traditional seven liberal arts; others feel that to ignore its connection to the sciences is to turn a blind eye to the fact that the interface between mathematics and its applications in science and engineering has driven much development in mathematics. One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematics is created (as in art) or discovered (as in science). It is common to see universities divided into sections that include a division of Science and Mathematics, indicating that the fields are seen as being allied but that they do not coincide. In practice, mathematicians are typically grouped with scientists at the gross level but separated at finer levels. This is one of many issues considered in the philosophy of mathematics.^{[citation needed]}

Fields of mathematics

An abacus, a simple calculating tool used since ancient times.

Mathematics can, broadly speaking, be subdivided into the study of quantity, structure, space, and change (i.e. arithmetic, algebra, geometry, and analysis).^{[citation needed]} In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.

Quantity

The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, from which come such popular results as Fermat's Last Theorem. Number theory also holds two problems widely considered to be unsolved: the twin prime conjecture and Goldbach's conjecture.
As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of "infinity". Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.

$1, 2, 3\,...\!$	$...-2, -1, 0, 1, 2\,...\!$	$-2, \frac{2}{3}, 1.21\,\!$	$-e, \sqrt{2}, 3, \pi\,\!$	$2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\,\!$
Natural numbers	Integers	Rational numbers	Real numbers	Complex numbers

Structure

Many mathematical objects, such as sets of numbers and functions, exhibit internal structure as a consequence of operations or relations that are defined on the set. Mathematics then studies properties of those sets that can be expressed in terms of that structure; for instance number theory studies properties of the set of integers that can be expressed in terms of arithmetic operations. Moreover, it frequently happens that different such structured sets (or structures) exhibit similar properties, which makes it possible, by a further step of abstraction, to state axioms for a class of structures, and then study at once the whole class of structures satisfying these axioms. Thus one can study groups, rings, fields and other abstract systems; together such studies (for structures defined by algebraic operations) constitute the domain of abstract algebra. By its great generality, abstract algebra can often be applied to seemingly unrelated problems; for instance a number of ancient problems concerning compass and straightedge constructions were finally solved using Galois theory, which involves field theory and group theory. Another example of an algebraic theory is linear algebra, which is the general study of vector spaces, whose elements called vectors have both quantity and direction, and can be used to model (relations between) points in space. This is one example of the phenomenon that the originally unrelated areas of geometry and algebra have very strong interactions in modern mathematics. Combinatorics studies ways of enumerating the number of objects that fit a given structure.

$\begin{matrix} (1,2,3) & (1,3,2) \\ (2,1,3) & (2,3,1) \\ (3,1,2) & (3,2,1) \end{matrix}$
Combinatorics	Number theory	Group theory	Graph theory	Order theory

Space

The study of space originates with geometry – in particular, Euclidean geometry. Trigonometry is the branch of mathematics that deals with relationships between the sides and the angles of triangles and with the trigonometric functions; it combines space and numbers, and encompasses the well-known Pythagorean theorem. The modern study of space generalizes these ideas to include higher-dimensional geometry, non-Euclidean geometries (which play a central role in general relativity) and topology. Quantity and space both play a role in analytic geometry, differential geometry, and algebraic geometry. Within differential geometry are the concepts of fiber bundles and calculus on manifolds, in particular, vector and tensor calculus. Within algebraic geometry is the description of geometric objects as solution sets of polynomial equations, combining the concepts of quantity and space, and also the study of topological groups, which combine structure and space. Lie groups are used to study space, structure, and change. Topology in all its many ramifications may have been the greatest growth area in 20th century mathematics; it includes point-set topology, set-theoretic topology, algebraic topology and differential topology. In particular, instances of modern day topology are metrizability theory, axiomatic set theory, homotopy theory, and Morse theory. Topology also includes the now solved Poincaré conjecture and the controversial four color theorem, whose only proof, by computer, has never been verified by a human.


Geometry	Trigonometry	Differential geometry	Topology	Fractal geometry	Measure Theory

Change

Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. The rigorous study of real numbers and functions of a real variable is known as real analysis, with complex analysis the equivalent field for the complex numbers. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many problems lead naturally to relationships between a quantity and its rate of change, and these are studied as differential equations. Many phenomena in nature can be described by dynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet still deterministic behavior.


Calculus	Vector calculus	Differential equations	Dynamical systems	Chaos theory	Complex analysis

Foundations and philosophy

In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic includes the mathematical study of logic and the applications of formal logic to other areas of mathematics; set theory is the branch of mathematics that studies sets or collections of objects. Category theory, which deals in an abstract way with mathematical structures and relationships between them, is still in development. The phrase "crisis of foundations" describes the search for a rigorous foundation for mathematics that took place from approximately 1900 to 1930.^[32] Some disagreement about the foundations of mathematics continues to present day. The crisis of foundations was stimulated by a number of controversies at the time, including the controversy over Cantor's set theory and the Brouwer-Hilbert controversy.
Mathematical logic is concerned with setting mathematics within a rigorous axiomatic framework, and studying the implications of such a framework. As such, it is home to Gödel's incompleteness theorems which (informally) imply that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarily incomplete (meaning that there are true theorems which cannot be proved in that system). Whatever finite collection of number-theoretical axioms is taken as a foundation, Gödel showed how to construct a formal statement that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a complete axiomatization of full number theory.^{[citation needed]} Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked to theoretical computer science.

$p \Rightarrow q \,$
Mathematical logic	Set theory	Category theory

Theoretical computer science

Theoretical computer science includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most powerful known model – the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. A famous problem is the "P=NP?" problem, one of the Millennium Prize Problems.^[33] Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.


Theory of computation	Cryptography

Applied mathematics

Applied mathematics considers the use of abstract mathematical tools in solving concrete problems in the sciences, business, and other areas.
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially with probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments; the design of a statistical sample or experiment specifies the analysis of the data (before the data be available). When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference – with model selection and estimation; the estimated models and consequential predictions should be tested on new data.^[34]
Computational mathematics proposes and studies methods for solving mathematical problems that are typically too large for human numerical capacity. Numerical analysis studies methods for problems in analysis using ideas of functional analysis and techniques of approximation theory; numerical analysis includes the study of approximation and discretization broadly with special concern for rounding errors. Other areas of computational mathematics include computer algebra and symbolic computation.


Mathematical physics	Fluid dynamics	Numerical analysis	Optimization	Probability theory	Statistics

Mathematical finance	Game theory	Mathematical biology	Mathematical chemistry	Mathematical economics	Control theory

Mathematics as profession

The best-known award in mathematics is the Fields Medal,^[35]^[36] established in 1936 and now awarded every 4 years. It is often considered the equivalent of science's Nobel Prizes. The Wolf Prize in Mathematics, instituted in 1978, recognizes lifetime achievement, and another major international award, the Abel Prize, was introduced in 2003. The Chern Medal was introduced in 2010 to recognize lifetime achievement. These are awarded for a particular body of work, which may be innovation, or resolution of an outstanding problem in an established field.
A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert. This list achieved great celebrity among mathematicians, and at least nine of the problems have now been solved. A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Solution of each of these problems carries a $1 million reward, and only one (the Riemann hypothesis) is duplicated in Hilbert's problems.